Linear Maps: The Basis Of Linear Algebra

Linear Maps: The Basis of Linear Algebra

Associated Articles: Linear Maps: The Basis of Linear Algebra

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Linear Maps: The Basis of Linear Algebra. Let’s weave fascinating data and supply recent views to the readers.

Linear Maps: The Basis of Linear Algebra

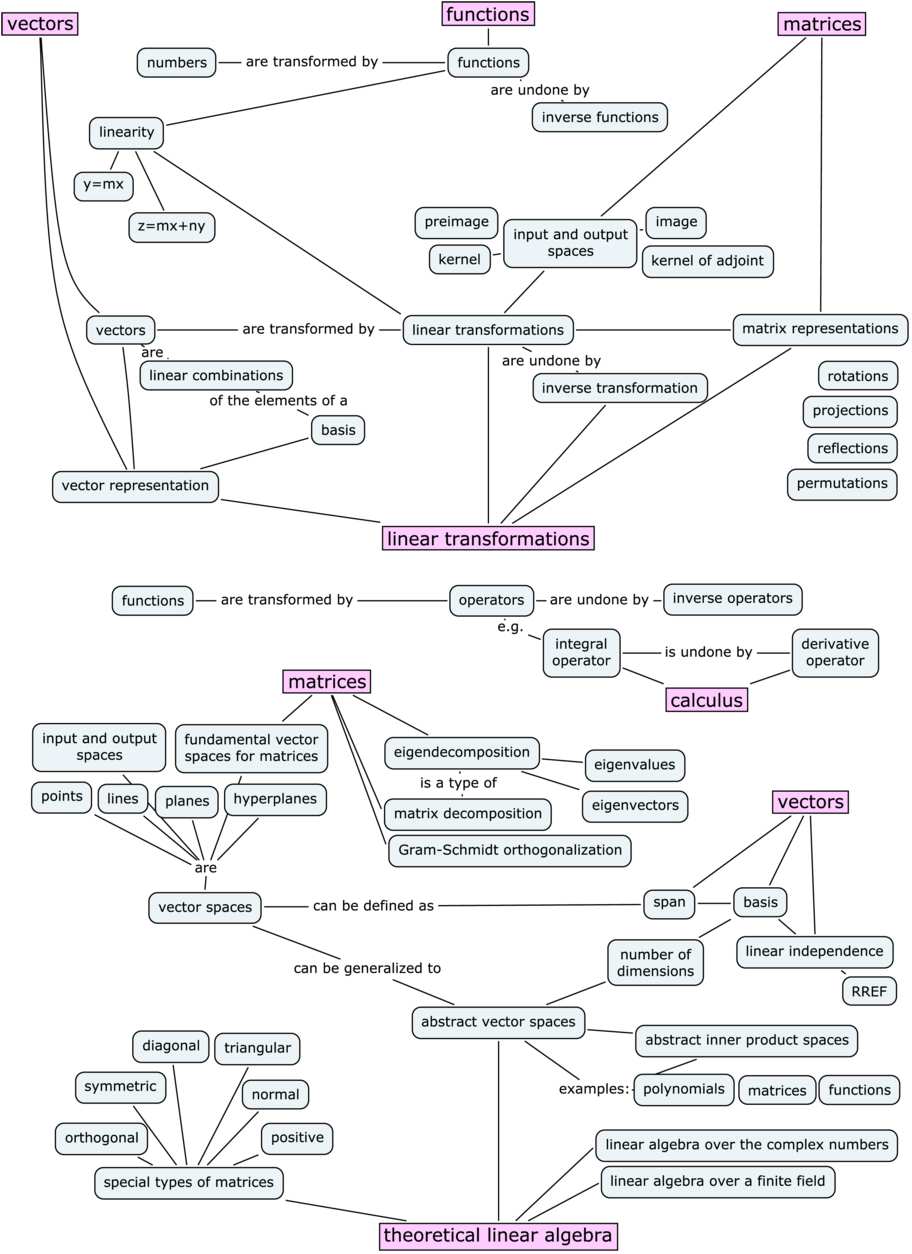
Linear maps, often known as linear transformations, are elementary objects in linear algebra. They characterize features that protect the operations of vector addition and scalar multiplication. Understanding linear maps is essential for greedy many core ideas in linear algebra, together with eigenvalues, eigenvectors, matrix representations, and the answer of linear methods. This text will delve into the definition, properties, and purposes of linear maps, offering a complete overview appropriate for college students and people in search of a deeper understanding of this important subject.

1. Definition and Properties

Let V and W be two vector areas over the identical discipline F (e.g., the actual numbers ℝ or the advanced numbers ℂ). A operate T: V → W is named a linear map (or linear transformation) if it satisfies the next two circumstances for all vectors u, v ∈ V and all scalars c ∈ F:

1. Additivity: T(u + v) = T(u) + T(v)
2. Homogeneity: T(cu) = cT(u)

These two circumstances may be mixed right into a single situation:

T(c₁u + c₂v) = c₁T(u) + c₂T(v) for all u, v ∈ V and c₁, c₂ ∈ F. This demonstrates the linearity – the transformation preserves linear combos.

Let’s illustrate this with a easy instance. Take into account the operate T: ℝ² → ℝ² outlined by:

T(x, y) = (2x + y, x – 3y)

To confirm if T is a linear map, we test the additivity and homogeneity properties:

Additivity: Let u = (x₁, y₁) and v = (x₂, y₂). Then:

T(u + v) = T(x₁ + x₂, y₁ + y₂) = (2(x₁ + x₂) + (y₁ + y₂), (x₁ + x₂) – 3(y₁ + y₂)) = (2x₁ + 2x₂ + y₁ + y₂, x₁ + x₂ – 3y₁ – 3y₂)

T(u) + T(v) = (2x₁ + y₁, x₁ – 3y₁) + (2x₂ + y₂, x₂ – 3y₂) = (2x₁ + 2x₂ + y₁ + y₂, x₁ + x₂ – 3y₁ – 3y₂)

Since T(u + v) = T(u) + T(v), the additivity property holds.

Homogeneity: Let u = (x, y) and c ∈ ℝ. Then:

T(cu) = T(cx, cy) = (2(cx) + cy, cx – 3(cy)) = (2cx + cy, cx – 3cy) = c(2x + y, x – 3y) = cT(u)

Since T(cu) = cT(u), the homogeneity property holds.

Subsequently, T(x, y) = (2x + y, x – 3y) is a linear map.

2. Kernel and Picture

Two essential subspaces related to a linear map T: V → W are its kernel (or null area) and its picture (or vary).

• Kernel (Ker(T)): The kernel of T is the set of all vectors in V which can be mapped to the zero vector in W:

Ker(T) = T(v) = 0

The kernel is all the time a subspace of V. If Ker(T) = 0, then T is injective (one-to-one), which means that distinct vectors in V are mapped to distinct vectors in W.

• Picture (Im(T)): The picture of T is the set of all vectors in W which can be the picture of some vector in V:

Im(T) = w ∈ W

The picture is all the time a subspace of W. If Im(T) = W, then T is surjective (onto), which means that each vector in W is the picture of no less than one vector in V.

A linear map that’s each injective and surjective is named an isomorphism. Isomorphisms set up a one-to-one correspondence between the vector areas V and W, preserving their linear construction.

3. Matrix Illustration of Linear Maps

Linear maps between finite-dimensional vector areas may be represented by matrices. Let V and W be vector areas with dimensions n and m, respectively, and let v₁, v₂, …, vₙ be a foundation for V and w₁, w₂, …, wₘ be a foundation for W. Then any linear map T: V → W may be represented by an m × n matrix A, the place the j-th column of A consists of the coordinates of T(vⱼ) with respect to the idea w₁, w₂, …, wₘ.

This matrix A permits us to compute the picture of any vector v ∈ V by matrix multiplication:

T(v) = Av

The selection of bases for V and W impacts the ensuing matrix A. A change of foundation ends in a similarity transformation of the matrix.

4. Functions of Linear Maps

Linear maps have widespread purposes throughout varied fields:

• Pc Graphics: Transformations like rotations, scaling, and shearing are linear maps. These are used extensively in pc graphics to govern photographs and 3D fashions.

• Picture Processing: Linear filters, akin to blurring and edge detection, are applied utilizing linear maps. These operations manipulate pixel values in a picture primarily based on linear combos of neighboring pixels.

• Machine Studying: Many machine studying algorithms rely closely on linear maps. As an illustration, linear regression includes discovering a linear map that finest approximates a given dataset. Neural networks make the most of linear maps of their layers to carry out transformations on enter knowledge.

• Quantum Mechanics: Quantum mechanical operators are sometimes represented as linear maps appearing on Hilbert areas. These operators describe the evolution and measurement of quantum methods.

• Differential Equations: Linear differential equations may be analyzed utilizing linear maps. The options to those equations typically kind vector areas, and the differential operator itself may be seen as a linear map.

• Cryptography: Linear algebra and linear maps play a vital function in varied cryptographic methods. As an illustration, linear transformations are used within the design of encryption and decryption algorithms.

5. Additional Ideas and Extensions

Past the fundamentals, a number of superior ideas construct upon the inspiration of linear maps:

• Eigenvalues and Eigenvectors: These are elementary ideas in linear algebra that characterize the habits of a linear map. Eigenvectors are vectors which can be solely scaled by the linear map, and the scaling issue is the eigenvalue. Eigenvalues and eigenvectors present insights into the dynamics of methods represented by linear maps.

• Singular Worth Decomposition (SVD): This highly effective factorization method decomposes a linear map right into a product of three matrices, revealing essential details about the map’s properties, together with its rank and nullity. SVD is broadly utilized in dimensionality discount and knowledge evaluation.

• Linear Useful: A linear useful is a linear map from a vector area V to its underlying discipline F. Linear functionals kind the twin area V*, which is itself a vector area.

• Linear Operators: A linear operator is a linear map from a vector area to itself (T: V → V). These are notably essential in finding out the properties of vector areas and their transformations.

• Multilinear Maps: These generalize linear maps to deal with a number of vector inputs. Examples embody bilinear varieties and tensor merchandise, that are essential in varied areas like differential geometry and physics.

6. Conclusion

Linear maps are a cornerstone of linear algebra, offering a robust framework for understanding and manipulating vector areas. Their properties, akin to additivity and homogeneity, be certain that linear combos are preserved underneath transformation. The ideas of kernel and picture characterize the injectivity and surjectivity of a linear map, whereas matrix representations enable for environment friendly computation. The widespread purposes of linear maps throughout various fields spotlight their significance in arithmetic, pc science, physics, and engineering. A radical understanding of linear maps is crucial for anybody pursuing superior research in these areas. Additional exploration of the superior ideas talked about above will present a extra full and nuanced appreciation of the richness and energy of this elementary mathematical object.

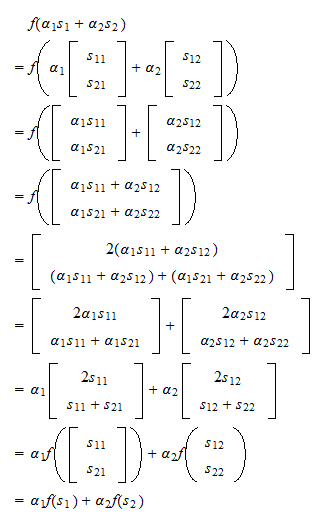
Closure

Thus, we hope this text has offered worthwhile insights into Linear Maps: The Basis of Linear Algebra. We admire your consideration to our article. See you in our subsequent article!